Tests de Student et analyse des résultats de sondages

L'analyse de résultats de sondage ne se résume pas à une comparaison de graphiques. Si nous sommes tous capables de constater une différence entre deux nombres, nous avons beaucoup plus de difficultés pour déterminer si cette différence est statistiquement significative ou non.

Imaginons, vous avez effectué un sondage de satisfaction client pour votre entreprise et vous vous retrouvez avec une montagne de résultats à analyser. Lorsque vous l'interrogez sur les données à analyser en priorité, votre responsable vous demande si les hommes et les femmes ont donné des réponses différentes. Par exemple, si les hommes vous ont attribué un Net Promoter Score℠ (NPS) moins élevé que les femmes.

Vos résultats montrent une évaluation moyenne de 9 pour les réponses des hommes et de 12 pour celles des femmes. Vous vous demandez comment interpréter cette différence ? Utilisez un test de Student !

Disponible sous différentes formes en fonction de la formule de calcul utilisée, ce test, également connu sous le nom de test-t, vous permet de déterminer si une différence entre deux nombres est vraiment significative d'un point de vue statistique.

1. Test de Student pour échantillon unique : ce test permet de détecter si la valeur moyenne des données d'un groupe (ici, le score NPS global) est différente d'une valeur définie par vos soins.

Exemple : votre entreprise a pour objectif d'obtenir un NPS nettement plus élevé que la norme du secteur, à savoir 5. Lors du dernier sondage, votre entreprise a obtenu un NPS égal à 10. Pouvez-vous considérer un NPS de 10 significativement plus élevé que 5, la norme du secteur ?

2. Test de Student pour échantillons indépendants : ce test permet de déterminer si les valeurs moyennes de deux groupes indépendants sont significativement différentes l'une de l'autre.

Exemple : en partant de votre hypothèse selon laquelle les hommes attribuent à votre entreprise un NPS moins élevé que les femmes. Avec un NPS moyen de 9 auprès des hommes et de 12 auprès des femmes, la différence entre 9 et 12 est-elle statistiquement significative ?

3. Test de Student apparié : utilisé lorsque l'on soumet deux fois le même sondage à un groupe de personnes, ce test permet de déterminer si la moyenne a évolué entre le premier et le second sondage.

Exemple : vous avez sondé le même groupe de clients à deux reprises, d'abord en avril, puis en mai, après qu'ils aient vu une publicité pour votre entreprise. Le NPS de votre entreprise a-t-il évolué entre avril et mai suite à cette publicité ?

Les tests de Student ou tests-t permettent de montrer une différence statistique, mais c'est à vous qu'il revient de décider si cette différence est significative. Même de légères différences peuvent être statistiquement significatives sur un échantillon suffisamment grand.

Un test de Student se déroule en quatre étapes :

1. Calcul de la statistique-t :
Chaque type de test de Student a sa propre formule de calcul de la statistique-t (retrouvez les formules pour chaque test de Student en fin d'article).

2. Calcul des degrés de liberté :
Les degrés de liberté correspondent au nombre de variances possibles de la moyenne. Dans notre exemple, les degrés de liberté correspondent au nombre d'évaluations NPS que vous pouvez obtenir dans un groupe de participants. Tout comme la statistique-t, la formule de calcul des degrés de liberté varie selon le type de test de Student effectué.

3. Détermination de la valeur critique :
La valeur critique est le seuil à partir duquel la différence entre deux nombres est considérée comme statistiquement significative.

4. Comparaison de la valeur absolue de la statistique-t avec la valeur critique :
Si la statistique-t est supérieure à la valeur critique, alors la différence est significative. Si la statistique-t est inférieure, il n'est pas possible de différencier les deux nombres d'un point de vue statistique.

Reprenons notre exemple initial : selon votre hypothèse, les hommes ont attribué à votre entreprise un score NPS moins élevé que les femmes. Le score NPS moyen attribué par les hommes s'élève à 9, celui attribué par les femmes à 12. La différence entre 9 et 12 est-elle statistiquement significative ? Dans cet exemple, il convient d'utiliser le test de Student pour échantillons indépendants.

1. Calcul de la statistique-t : 

La formule ci-dessous vous permet de calculer la statistique-t lors d'un test de Student pour échantillons indépendants, où :

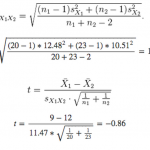
2. Calcul des degrés de liberté : 

Utilisez la formule ci-dessous pour déterminer les degrés de liberté dans les tests de Student pour échantillons indépendants. (Les formules de calcul pour les autres types de test de Student sont fournies plus loin dans l'article.)

3. Détermination de la valeur critique : 

Selon ce tableau, la valeur critique pour un test de Student pour échantillons indépendants avec un niveau alpha de 0,05 à 41 degrés de liberté est égale à 2,02. Notez que la plupart des analystes préfèrent le test de Student pour échantillons indépendants au test pour échantillon unique, car il est considéré comme plus conservateur. Apprenez-en plus sur les différences entre tests de Student pour échantillons indépendants et tests de Student pour échantillon unique dans cette vidéo de la Khan Academy.

4. Comparaison de la valeur absolue de la statistique-t avec la valeur critique : 

Étant donné que la valeur absolue de la statistique-t est égale à 0,86 et qu'elle est par conséquent inférieure à la valeur critique 2,02, vous pouvez en conclure que l'évaluation NPS attribuée par les hommes n'est pas significativement inférieure à l'évaluation attribuée par les femmes.

Vous pouvez utiliser une feuille de calcul ou un logiciel de statistiques (comme Excel ou SPSS) pour réaliser les tests-t, mais si vous souhaitez effectuer les calculs manuellement, reprenez la formule du test de Student ci-dessous en fonction du test effectué.

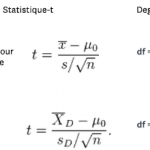
Si vous optez (comme la plupart des utilisateurs) pour une feuille de calcul ou un logiciel de statistiques pour effectuer vos tests de Student, la procédure sera légèrement différente. Au lieu de comparer la statistique-t avec la valeur critique, la plupart des programmes calculent une valeur p qu'ils comparent avec votre niveau alpha (le niveau le plus fréquemment utilisé étant 0,05). Si la valeur p est inférieure à votre niveau alpha, vous pouvez conclure que la différence entre les nombres est statistiquement significative.

« Net Promoter Score » est une marque commerciale de Bain & Company, Inc, Satmetrix Systems, Inc. et F. Reichheld.