Suivez le guide : calculateur de la valeur p
Vos données sont-elles suffisantes pour rejeter l'hypothèse nulle ? Calculez facilement une valeur p à l’aide de notre calculateur.
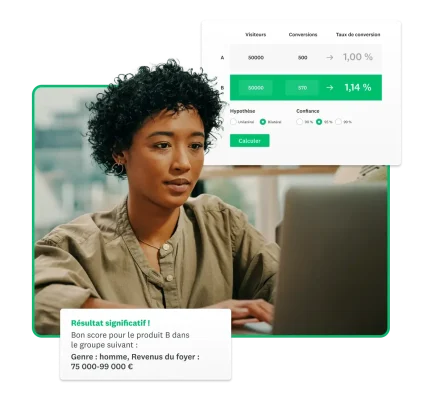
Calculateur de valeur p
Score Z
Type de test
Niveau de signification
Valeur p =
0
Le résultat n'est pas significatif lorsque p ≥
0.05
Imaginez : vous plongez dans le monde de l’analyse et des statistiques, en essayant de donner un sens à toutes ces données. Et là, vous tombez sur une petite merveille appelée la valeur p. C’est comme un code secret. Les chercheurs l’utilisent pour percer des mystères, vérifier des hypothèses et analyser leur signification.
La valeur p est principalement utilisée pour guider la prise de décision dans le cadre de la vérification d’hypothèse. Elle aide les chercheurs à évaluer si les données observées sont suffisantes pour rejeter l’hypothèse nulle, au profit d’une autre hypothèse. Ils s’appuient également sur la valeur p pour comparer des groupes ou tester des corrélations.
Trouvez des réponses à vos questions avec le calculateur de valeur p de SurveyMonkey ci-dessus.
Qu’est-ce qu’une valeur p ?
La valeur p est une valeur de probabilité. Elle mesure la probabilité d’un résultat, en partant du principe que l’hypothèse nulle est vraie. Elle constitue un indicateur de probabilité qui montre dans quelle mesure votre résultat est probable, en supposant qu’il n’y a pas de différence réelle (l’hypothèse nulle).
La valeur p quantifie la solidité de la preuve contre l’hypothèse nulle. Elle est généralement comparée à un niveau de signification prédéterminé, par exemple 0,05. Si la valeur p est faible, cela signifie que l’hypothèse est probablement justifiée. Vous pouvez donc en toute confiance rejeter l’hypothèse nulle et supposer que votre hypothèse est vraie.
La valeur p est primordiale : les chercheurs s’appuient sur cette donnée pour accepter ou rejeter l’hypothèse nulle. Voici quelques exemples de questions de recherche pour lesquelles la valeur p peut être utilisée :
- « Les hommes et les femmes diffèrent-ils en matière de satisfaction de la clientèle ? »
- « La satisfaction à l’égard des programmes de formation est-elle en lien avec la satisfaction des employés ? »
Une valeur p faible est le signe de disparités entre les groupes évalués. Elle montre également qu’il peut exister des relations réelles et prévisibles entre les variables.
Les chercheurs peuvent alors interpréter la signification de leurs conclusions et communiquer la solidité de la preuve aux différentes parties prenantes.
Comment calculer la valeur p ?
Pour calculer une valeur p, il faut d’abord déterminer la probabilité d’obtenir les données si l’hypothèse nulle était vraie. Ensuite, il convient de comparer cette probabilité au niveau de signification choisi (généralement 0,05) pour décider si vos résultats sont statistiquement significatifs.
Calculez la valeur p à partir du score z
Pour calculer une valeur p à partir d’un score z, recherchez le score z dans une table de distribution normale standard. Vous pouvez également utiliser un logiciel pour trouver la probabilité correspondante. Cette probabilité représente la vraisemblance d’observer une valeur aussi extrême que le score z sous l’hypothèse nulle.
La valeur p peut être calculée à l’aide des formules suivantes :
- Test z unilatéral à gauche : valeur p = P(score z)
- Test z unilatéral à droite : valeur p = 1 - P(score z)
- Test z bilatéral : valeur p = 2 × P(-|score z|) ou 2 - 2 × P(|score z|)
Voici les différentes étapes à suivre pour calculer la valeur p à partir d’un score z :
- Comprendre le problème : vous disposez de données et souhaitez connaître la probabilité d’obtenir un résultat spécifique. Vous souhaitez également déterminer la probabilité d’une situation extrême, en supposant que l’hypothèse nulle est vraie.
- Trouver le score z : commencez par déterminer le score z de vos données. Il vous indique le nombre d’écarts types entre votre point de données et la moyenne. Trouvez votre score z en utilisant un logiciel d’analyse statistique (comme R ou SPSS) ou recherchez l’écart dans une table (comme celle-ci).
- Déterminer la direction : choisissez un test unilatéral (valeurs extrêmes dans un sens) ou un test bilatéral (dans les deux sens). Si vous pensez que la différence sera significativement plus petite ou plus grande, utilisez un test unilatéral (test à gauche ou à droite). En l’absence d’hypothèse sur le sens de la différence, optez pour un test bilatéral.
- Trouver le score z : à l’aide d’une table normale standard, d’un logiciel ou d’une calculatrice de valeur p, trouvez la probabilité cumulée.
- Calculez la valeur p en utilisant le calculateur de valeur p ci-dessus, ou via l’une des méthodes suivantes :
- Pour un test unilatéral : si le score z est positif (test unilatéral à droite), soustrayez la probabilité cumulée de 1. Si le score z est négatif (test unilatéral à gauche), utilisez directement la probabilité cumulative.
- Pour un test bilatéral : multipliez par 2 la probabilité cumulative pour tenir compte des deux directions. Puis, si le score z est positif, soustrayez cette probabilité au chiffre 1.
- Interpréter la valeur p : si la valeur p est très faible (généralement inférieure à 0,05), cela montre que vos données ne sont pas susceptibles de correspondre à l’hypothèse nulle, ce qui indique une signification statistique. Vous pouvez également utiliser notre calculateur de valeur p ci-dessus pour interpréter la valeur p en fonction du niveau de confiance.
Calculez la valeur p à partir du score t
Pour calculer une valeur p à partir d’un score t, déterminez d’abord le score t, qui représente la différence entre la moyenne de votre échantillon et celle de la population. Utilisez ensuite une table de distribution t ou un logiciel pour déterminer ce score t. Ce score indique la probabilité d’obtenir les résultats de votre échantillon sous l’hypothèse nulle.
La formule suivante vous permet d’obtenir la valeur p à partir du score t.
- Test t unilatéral à droite : valeur p = cdft,d(score t)
- Test t unilatéral à gauche : valeur p = 1 - cdft,d(score t)
- Test t bilatéral : valeur p = 2 × cdft,d(-|score t|) ou valeur p = 2 - 2 × cdft,d(|score t|)
Où cdft,d représente la fonction de distribution cumulative de la distribution t de Student avec d degrés de liberté.
Voyons ensemble les différentes étapes à suivre pour calculer la valeur p à partir d’un score t.
- Comprendre la situation : vous disposez d’un échantillon de données et souhaitez connaître la probabilité d’obtenir vos résultats. Cela suppose qu’il n’y a pas de différence réelle dans la population.
- Calculer le score t : cette mesure vous indique la différence entre la moyenne de votre échantillon et celle de la population.
- Déterminer les degrés de liberté : ils dépendent de la taille de votre échantillon. Cela vous aide à trouver la probabilité correcte dans la table de distribution t.
- Consulter la table de distribution t : cherchez le score t que vous avez calculé dans cette table. Cela vous donne la probabilité d’observer cette différence ou une différence plus importante en l’absence de différence réelle dans la population.
- Interpréter le résultat : si la valeur p est très faible, les résultats de votre échantillon sont peu probables sous l’hypothèse nulle. Cela suggère que vos résultats pourraient être significatifs.
Calculez la valeur p à partir de la corrélation de Pearson
Pour déterminer la valeur p pour un coefficient de corrélation de Pearson, il faut d’abord utiliser le coefficient calculé pour obtenir une statistique t. Vous pouvez ensuite trouver la valeur p associée en utilisant la distribution t avec des degrés de liberté (n - 2).
La formule pour obtenir la statistique t à partir d’un coefficient de corrélation de Pearson est la suivante :

Où :
- r est le coefficient de corrélation de Pearson
- n est la taille de l’échantillon
Après avoir obtenu la statistique t, vous pouvez calculer la valeur p à l’aide de la fonction de distribution cumulative de la distribution t. Cette méthode utilise n - 2 degrés de liberté, où n est la taille de l’échantillon.
Voici la méthode générale :
- Comprendre la situation : vous disposez d’un échantillon de données et souhaitez déterminer si deux variables sont corrélées.
- Calculer la statistique t : convertissez le coefficient de corrélation (r) en une statistique t à l’aide de la formule ci-dessus.
- Déterminer les degrés de liberté : calculer les degrés de liberté (df). Utilisez la formule df = n - 2, où n est la taille de l’échantillon.
- Trouver la valeur p : une fois que vous disposez de la statistique t et des degrés de liberté, vous pouvez utiliser une table de distribution t ou un logiciel statistique pour trouver la valeur p associée à la statistique t calculée.
- Interpréter le résultat : si la valeur p est inférieure au seuil de signification choisi (généralement 0,05), vous rejetez l’hypothèse nulle et concluez qu’il existe une corrélation statistiquement significative entre les deux variables. Dans le cas contraire, vous ne pouvez pas rejeter l’hypothèse nulle.
Calculez la valeur p à partir de la valeur du khi carré
Pour calculer la valeur p d’une valeur du khi carré, déterminez les degrés de liberté associés à la distribution du khi carré. Utilisez ensuite des tableaux ou des logiciels statistiques pour trouver la probabilité d’obtenir une valeur du khi carré aussi extrême que celle observée.
Vous pouvez obtenir la valeur p à l’aide de la formule suivante :
valeur p=1− cdfχ² (x; df)
Où :
- x est la statistique du test khi carré.
- cdfχ² est la fonction de distribution cumulative de la distribution du khi carré.
- df est le degré de liberté.
La probabilité cumulée est soustraite de 1, car la distribution du khi carré est asymétrique, de sorte que la zone à droite de la valeur observée du khi carré correspond à la valeur p.
Voici les étapes à suivre pour calculer la valeur p à partir d’une valeur du khi carré :
- Comprendre la situation : vous disposez de données catégorielles et souhaitez déterminer s’il existe des associations significatives entre les variables.
- Calculer la valeur du khi carré.
- Déterminer les degrés de liberté (df) : les degrés de liberté sont déterminés par le nombre de catégories moins 1 pour un simple test khi carré. Pour un test d’indépendance du khi carré, le calcul est (lignes−1)×(colonnes−1).
- Trouver la valeur p : utilisez des tableaux statistiques ou des logiciels pour trouver la probabilité cumulative pour le khi carré et les degrés de liberté. Il s’agit de la zone située à droite de la valeur du khi carré sous la courbe de distribution du khi carré.
- Interpréter le résultat : comparez la valeur p obtenue au seuil de signification choisi (généralement 0,05). Si la valeur p est inférieure au seuil de signification, vous rejetez l’hypothèse nulle et concluez qu’il existe des liens significatifs entre les variables. Dans le cas contraire, vous ne pouvez pas rejeter l’hypothèse nulle.
Comment interpréter la valeur p ?
Si la valeur p est inférieure ou égale à 0,05 (ou à tout autre niveau de signification choisi), alors le résultat est statistiquement significatif. Cela montre que le résultat observé est significatif au niveau α.
Donc la probabilité d’obtenir un résultat extrême, en supposant que l’hypothèse nulle soit vraie, est très faible. En règle générale, cette probabilité est inférieure à 5 %.
Par conséquent, vous rejetez l’hypothèse nulle en faveur de l’autre hypothèse. Cela indique que des preuves corroborent l’affirmation de l’autre hypothèse.
Si la valeur p est supérieure à 0,05, alors le résultat observé n’est pas statistiquement significatif au niveau de signification choisi. En d’autres termes, il n’y a pas suffisamment de preuves pour rejeter l’hypothèse nulle. Nous ne pouvons donc pas conclure que le résultat observé diffère de ce que l’on attendrait sous l’hypothèse nulle.
À lire aussi : Comment analyser vos données de sondage ?
Erreurs courantes concernant la valeur p
Utiliser la valeur p pour représenter des probabilités réelles
Certaines personnes pensent qu’une valeur p de 0,05 signifie qu’il y a 95 % de chances que l’hypothèse du test soit vraie et 5 % de chances qu’elle soit fausse. Il s’agit d’une interprétation erronée de la valeur p.
Les valeurs p indiquent la probabilité d’observer les données en supposant que l’hypothèse nulle est vraie. Elles ne sont pas des mesures directes de la probabilité que les hypothèses soient vraies ou fausses.
Comprendre la valeur p comme la taille d’un effet ou l’importance d’un résultat
Considérer que la valeur p est synonyme de la taille de l’effet ou de l’importance d’un résultat est une idée fausse très répandue. Cela gomme la distinction entre la signification statistique et la signification pratique.
Une valeur p faible signifie que le résultat observé n’est probablement pas dû au hasard. Cependant, cela n’indique en rien l’ampleur de l’effet, ni ne reflète la pertinence pratique de cet effet.
Par exemple, même des écarts minimes par rapport à l’hypothèse nulle peuvent produire des valeurs p statistiquement significatives dans de vastes ensembles de données, bien qu’elles soient pratiquement insignifiantes. De même, si une expérience produit des différences significatives à plusieurs reprises, il est probable que l’on observe parfois des résultats non significatifs, car tout repose sur des probabilités.
Inversement, une valeur p élevée n’implique pas nécessairement que l’effet observé est insignifiant. Elle suggère plutôt que les données ne fournissent pas de preuves convaincantes que l’hypothèse nulle n’est pas vraie.
Pour évaluer avec précision l’importance pratique des résultats, il est essentiel de compléter les valeurs p par des mesures de la taille de l’effet. La taille de l’effet mesure l’ampleur de l’effet observé. Elle aide les chercheurs à replacer les résultats en contexte dans le cadre plus large de la question d’étude ou du champ d’application.
Cette distinction garantit que la signification statistique correspond à des implications significatives dans le monde réel. Elle éclaire la prise de décision et informe l’interprétation des résultats de la recherche.
Ne pas prendre en compte des tests multiples
Le problème des tests multiples se pose lorsque les chercheurs effectuent de nombreux tests d’hypothèse sur le même ensemble de données, sans ajuster le niveau de signification en conséquence. Cette pratique augmente considérablement la probabilité de faux positifs, également appelés « erreurs de type I ». Dans ce cas, l’hypothèse nulle est rejetée à tort.
Imaginez un scénario dans lequel plusieurs tests indépendants sont menés simultanément. Même si chaque test conserve un niveau de signification faible (par exemple, α = 0,05), la probabilité cumulée d’observer au moins un résultat significatif par le seul effet du hasard augmente. Ce phénomène se produit lorsque le nombre de tests augmente.
Les chercheurs utilisent des méthodes de correction statistique telles que la correction de Bonferroni pour rendre plus difficile le rejet de l’hypothèse nulle. Ces solutions permettront de contrôler rigoureusement le taux global de faux positifs. Elles garantissent que la probabilité de faux positifs pour l’ensemble des tests reste inférieure au seuil spécifié.
Les bonnes pratiques concernant l’analyse de la valeur P
Interprétez vos résultats en contexte
Examinez les implications pratiques de vos conclusions dans le contexte plus large de votre question d’étude ou champ d’application. Évitez de surinterpréter les résultats statistiquement significatifs ou d’écarter les résultats non significatifs sans un examen approfondi.
Supposons que vous constatiez une amélioration statistiquement significative des notes des élèves ayant suivi une nouvelle méthode d’enseignement. Cette amélioration est comparée aux notes obtenues avec la méthode traditionnelle.
Il faut éviter de surinterpréter les résultats, et plutôt prendre en compte des facteurs tels que la taille de l’effet. L’amélioration des notes est-elle suffisamment importante pour justifier la mise en œuvre de la nouvelle méthode d’enseignement à grande échelle ? Ce résultat pourrait-il être reproduit dans d’autres études avec des conditions similaires ? Faut-il considérer d’autres facteurs, tels que le coût ?
Inversement, des résultats non significatifs peuvent être dus à d’autres facteurs, tels qu’un échantillon de petite taille ou une erreur de mesure.
Il est donc important d’évaluer de manière critique la conception de l’étude, la qualité des données et les sources potentielles de biais avant de tirer des conclusions.
Prenez en compte toutes les valeurs p
Quelle que soit leur signification, il convient d’inclure toutes les valeurs p pour toutes les variables d’une étude. Cela vous donnera une vision globale de l’analyse. Vous donnerez aussi aux lecteurs la possibilité d’évaluer la fiabilité de vos conclusions.
En communiquant toutes les valeurs p, les chercheurs présentent l’ensemble des analyses statistiques, y compris celles dont les résultats ne sont pas significatifs. Cette transparence permet aux lecteurs d’évaluer la cohérence et la fiabilité des conclusions entre les différentes variables et analyses. Cela favorise également l’intégrité de la recherche, car les données sont présentées dans leur intégralité, sans biais ni distorsion.
Faites preuve de prudence face à des valeurs p faibles
Il est capital de faire preuve de vigilance lorsque vous interprétez des valeurs p faibles. Cela peut parfois donner une idée trompeuse de la signification des effets observés.
Rappelez-vous bien que des effets réels et des échantillons de grande taille peuvent donner des valeurs p faibles. Les échantillons de grande taille augmentent l’efficacité statistique pour déceler des écarts insignifiants par rapport à l’hypothèse nulle.
Par conséquent, des valeurs p faibles dans des études avec des échantillons de grande taille ne sont pas nécessairement le reflet d’effets significatifs réels ou pratiques.
FAQ sur la valeur p
- Qu’est-ce qu’un score z ?
- Qu’est-ce qu’un score t ?
- Qu’est-ce qu’un score de Pearson ?
- Qu’est-ce que la valeur du khi carré ?
Autres ressources à votre disposition

Des solutions adaptées à votre rôle
Avec SurveyMonkey, maximisez l’impact de vos stratégies marketing, du développement de vos produits, de vos expériences client et plus encore.

Modèles de sondages
Créez et envoyez rapidement des sondages efficaces et attrayants grâce à SurveyMonkey et ses + de 400 modèles personnalisables et prêts à l’emploi.

Tout savoir sur les sondages avec chargement de fichier
Apprenez à utiliser un sondage avec fichier téléversé pour recueillir des informations supplémentaires et découvrez de nombreux exemples de questions.

Analyse multisondage : notre fonctionnalité tant attendue !
Avec la fonctionnalité Analyse multisondage de SurveyMonkey, combinez et analysez les résultats de plusieurs sondages.