Marge d’erreur : définition, calcul et exemples
Découvrez les rouages permettant de déterminer la marge d’erreur d’un sondage, et utilisez notre calculatrice en ligne pour la mesurer en quelques clics.
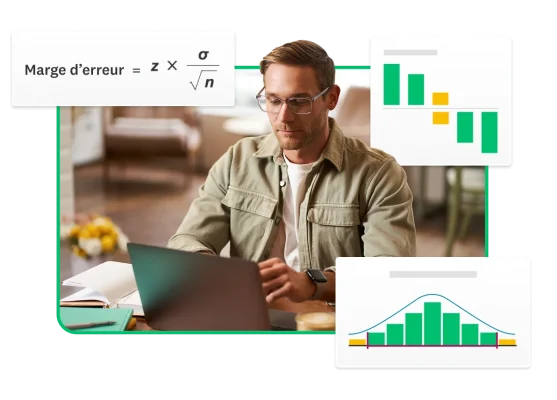
- La marge d’erreur évalue l’incertitude associée à un sondage, en indiquant dans quelle mesure les résultats obtenus pour un échantillon de personnes peuvent différer de ceux concernant la population globale.
- Elle se calcule à l’aide des 3 variables suivantes : n = la taille de l’échantillon • σ = l’écart-type de la population • z = le score z (le plus simple étant d’utiliser notre outil de calcul ci-dessous).
- La calculatrice de marge d’erreur vous permettra de déterminer si la taille de votre échantillon est suffisante pour garantir la fiabilité des données collectées.
Calculez votre marge d’erreur
Taille de la population
Niveau de confiance (%)
Taille de l’échantillon
Marge d’erreur
0
Qu’est-ce que la marge d’erreur ?
L’art du sondage s’apparente à un exercice d’équilibriste : vous vous appuyez sur un petit groupe de personnes (les participants au sondage) pour en déduire des informations sur un groupe beaucoup plus important (votre marché cible, ou la population totale). La marge d’erreur est une valeur statistique qui indique dans quelle mesure les résultats de votre sondage sont susceptibles de refléter l’opinion de la population totale.
La marge d’erreur évalue le degré de précision de votre sondage. Plus elle est faible, plus vous pouvez considérer que vos résultats sont fiables. Plus elle est élevée, plus vos résultats risquent de diverger de l’opinion de la population totale.
La marge d’erreur correspond à une plage de valeurs associées aux résultats d’un sondage. Par exemple, si un sondage montre que 60 % des personnes interrogées ont répondu « Oui » à une question, avec une marge d’erreur de 5 % et un niveau de confiance de 95 %, cela signifie qu’il y a 95 % de chances que 55 à 65 % de la population pense « Oui ».
La marge d’erreur est essentielle en recherche et dans l’analyse des sondages, car elle vous renseigne sur le niveau de fiabilité des résultats. La marge d’erreur permet de mieux comprendre l’incertitude associée aux résultats, et vous guide dans leur interprétation. Plus elle est faible, plus les résultats peuvent être considérés comme précis et fiables. Plus la marge d’erreur est importante, plus la variabilité et l’incertitude sont élevées.
Connaître la marge d’erreur vous permet de prendre des décisions éclairées en fonction de la fiabilité des données.
Qu’est-ce que l’intervalle de confiance ?
L’intervalle de confiance correspond à la plage de valeurs dans laquelle il est raisonnable de penser que se situe la vraie valeur. Par exemple, si nous cherchons à déterminer la taille moyenne des adultes d’un pays, l’intervalle de confiance indique la plage de valeurs dans laquelle nous sommes à peu près sûrs que se trouve la taille moyenne réelle.
L’intervalle de confiance permet aux chercheurs et aux décisionnaires de mieux comprendre l’incertitude associée à leurs estimations et leurs analyses.
Lien entre marge d’erreur et intervalle de confiance
L’intervalle de confiance et la marge d’erreur sont globalement deux moyens d’exprimer la même notion, à savoir le degré d’incertitude associé à une hypothèse. L’intervalle de confiance correspond à la plage de valeurs dans laquelle nous pensons que se trouve la valeur réelle. La marge d’erreur mesure l’écart potentiel entre notre hypothèse et la valeur réelle.
Concept connexe, mais différent, le niveau de confiance indique la probabilité selon laquelle la valeur réelle se trouve dans l’intervalle de confiance.
Les niveaux de confiance utilisés en référence sont souvent 90 %, 95 % ou 99 %. Utiliser un niveau de confiance moins élevé (comme 90 %) signifie que l’intervalle de confiance sera plus étroit et l’estimation plus précise, mais aussi qu’il y aura moins de chances que cette estimation reflète la valeur réelle. À l’inverse, avec un niveau de confiance plus élevé (comme 99 %), l’intervalle de confiance sera plus large et moins précis, mais il y aura plus de chances qu’il inclue la valeur réelle.
Pourquoi calculer la marge d’erreur ?
En planifiant votre sondage, vous devez évaluer la marge d’erreur afin de garantir la précision et la fiabilité de vos résultats. Ce calcul vous permettra de déterminer la taille d’échantillon nécessaire pour atteindre le degré de précision que vous souhaitez. Plus la marge d’erreur est faible, plus la taille de votre échantillon devra être importante. À l’inverse, plus la marge d’erreur est élevée, plus l’échantillon sera réduit.
Par exemple, si un chercheur veut effectuer un sondage sur une population de 100 000 personnes avec une marge d’erreur de ±5 % et un niveau de confiance de 95 %, il aura besoin d’un échantillon de 383 participants (calcul basé sur des formules standard).
La marge d’erreur est essentielle pour interpréter les résultats d’un sondage. En effet, elle permet d’évaluer leur fiabilité en quantifiant l’incertitude associée à ces résultats.
Par exemple, si un sondage indique que 60 % des personnes interrogées préfèrent le produit A au produit B, avec une marge d’erreur de ±3 % et un intervalle de confiance de 95 %, cela signifie qu’il y a une forte probabilité (95 %) que le pourcentage réel de personnes qui préfèrent le produit A se situe entre 57 et 63 %.
Comment calculer la marge d’erreur ?
La marge d’erreur se calcule à l’aide de la formule suivante :

n = taille de l’échantillon • σ = écart-type de la population • z = z-score
- Calculez l’écart-type de la population (σ) et la taille de l’échantillon (n). L’outil de calcul utilise un écart-type basé sur la racine carrée de p(1-p), où p correspond à la proportion de l’échantillon et est égal par défaut à 0,5.
- Divisez l’écart-type de votre population par la racine carrée de la taille de votre échantillon.
- Multipliez le résultat par la valeur du score z correspondant au niveau de confiance souhaité, en vous reportant au tableau ci-dessous.
| Niveau de confiance souhaité | z-score |
| 80 % | 1,28 |
| 85 % | 1,44 |
| 90 % | 1,65 |
| 95 % | 1,96 |
| 99 % | 2,58 |
Exemple de calcul de la marge d’erreur
Supposons que vous hésitiez entre le Nom A et le Nom B pour nommer un nouveau produit. Votre marché cible se compose de 400 000 clients potentiels. Il s’agit de votre population totale.
Parmi ces clients potentiels, vous décidez d’en sonder 600. Il s’agit de la taille de votre échantillon.
À la lumière des résultats de votre sondage, 60 % des personnes interrogées déclarent préférer le Nom A. Dans l’outil de calcul de marge d’erreur, vous devez saisir un niveau de confiance.
Ce nombre exprime à quel point vous pensez que votre échantillon reflète fidèlement l’avis de la population totale. Les spécialistes le fixent généralement à 90 %, 95 % ou 99 %.
Saisissez les chiffres de cet exemple dans l’outil de calcul ci-dessus. Vous obtenez une marge d’erreur de 4 %.
Vous vous souvenez que 60 % des participants à votre sondage avaient choisi le Nom A ? Cette marge d’erreur signifie que, selon une probabilité de 95 %, 56 à 64 % de la population totale (votre marché cible) préfère le Nom A pour ce produit.
Nous avons obtenu 56 et 64 en ajoutant et en soustrayant la marge d’erreur aux réponses de votre échantillon.
Comment interpréter la marge d’erreur ?
La marge d’erreur correspond à une plage de valeurs qui quantifie un niveau d’incertitude associé à une estimation dans un sondage. Par exemple, si un sondage indique que 60 % des personnes interrogées soutiennent une certaine politique, avec une marge d’erreur de ±4 % et un intervalle de confiance de 95 %, nous pouvons raisonnablement penser que le pourcentage de soutien réel se situe entre 56 et 64 %.
Quels facteurs influencent la marge d’erreur ?
1. Taille de l’échantillon
La taille de l’échantillon a une incidence directe sur la marge d’erreur. Avec des échantillons de taille importante, la marge d’erreur est généralement faible, tandis qu’avec des échantillons plus réduits, la marge d’erreur est plus élevée.
Par exemple, un sondage portant sur 1 000 participants pourrait avoir une marge d’erreur de ±3 %. En doublant la taille de l’échantillon (soit 2 000 participants), la marge d’erreur pourrait être réduite à ±2 %.
À lire aussi : Calculatrice de la taille d’échantillon
2. Niveau de confiance
Plus le niveau de confiance est élevé, plus la marge d’erreur est importante. Et plus il est bas, plus la marge d’erreur est faible.
Par exemple, on peut imaginer qu’un sondage avec un niveau de confiance de 95 % ait une marge d’erreur de ±3 %. En augmentant le niveau de confiance à 99 %, la marge d’erreur pourrait passer à ±4 %.
3. Variabilité de la population
Plus la variabilité de la population est importante, plus la marge d’erreur est élevée. Et moins elle est importante, plus la marge d’erreur est faible.
Par exemple, pour estimer le niveau de vie dans une ville où les revenus sont très hétérogènes, la marge d’erreur pourra être importante (±5 000 € par exemple). En revanche, pour une ville où les revenus sont plus homogènes, la marge d’erreur pourra être moins élevée (±2 000 € par exemple).
Améliorez la fiabilité de vos résultats

Maintenant que vous savez comment calculer la marge d’erreur et de quelle manière elle influence vos résultats, voyons comment utiliser ces concepts dans vos sondages.
1. Définissez votre population totale
Il s’agit de l’ensemble des personnes que vous voulez étudier dans votre sondage. Dans notre exemple précédent, il s’agissait des 400 000 clients potentiels.
2. Déterminez le niveau de risque
Vous devez décider jusqu’à quel point vous êtes prêt à risquer d’obtenir des résultats différents des comportements du marché cible global. Pour le déterminer, il vous faut évaluer la marge d’erreur et le niveau de confiance de votre échantillon.
3. Déterminez la taille de l’échantillon
En fonction du niveau de confiance que vous souhaitez et de la marge d’erreur qui vous semble acceptable, vous pourrez déterminer le nombre de participants dont vous avez besoin. Dites-vous bien que toutes les personnes ayant reçu votre sondage n’y répondront pas forcément. La taille de votre échantillon correspond au nombre de réponses complètes que vous recevrez.
4. Calculez le taux de réponse
Il s’agit du nombre de participants ayant répondu entièrement au sondage par rapport au nombre de personnes qui l’ont reçu. Reportez-vous aux taux de réponse obtenus lors de vos précédents sondages. Si vous n’avez aucun point de référence, faites une estimation. Pour être prudent, pouvez supposer que 10 à 15 % des participants répondront à l’intégralité de votre sondage.
5. Sondez votre public cible
Une fois que vous avez déterminé votre taux de réponse (étape 4), vous savez à combien de personnes vous devez envoyer votre sondage pour recevoir suffisamment de réponses complètes (étape 3). Comme nous l’avons vu plus haut, la marge d’erreur est un élément important pour concevoir un sondage bien équilibré. Après avoir calculé votre marge d’erreur (ainsi que les concepts associés, tels que la taille de l’échantillon et le niveau de confiance), vous pourrez commencer votre étude sur des bases solides.
À lire aussi : Comment estimer votre population cible ?
Améliorez votre marge d’erreur avec SurveyMonkey
Avec SurveyMonkey, vous pouvez facilement réduire votre marge d’erreur en augmentant la taille votre échantillon. Grâce à SurveyMonkey Audience, collectez rapidement des données de qualité auprès d’une population représentative de votre marché cible. Que vous souhaitiez lancer un nouveau produit, mesurer la satisfaction de vos clients ou mener des recherches académiques, cette puissante plateforme vous permettra de toucher votre public cible et d’obtenir de précieuses informations.
Collectez des données pertinentes
SurveyMonkey rassemble des outils simples et efficaces pour créer, optimiser et partager vos sondages, afin de recueillir les données dont vous avez besoin.